Улыбка волатильности vs Распределение вероятностей
Итак, имея информацию о ценах на опционы (берём цены прямо с рынка, из стакана) мы можем, пользуясь формулой Блэка-Шоулза, перевести их в график подразумеваемой волатильности для всех страйков, и воспроизвести улыбку IV. Насколько полезна для целей обычного трейдера данная информация? Практика показывает, что информация полезна, но можно добиться большего. Можно из информации о ценах на опционы восстановить распределение вероятностей, где окажется цена БА на дату экспирации. Для этого нам понадобится использовать какую-нибудь модель ценообразования опционов. Возьмем шестипараметрическую модель ABCDES, которую использует биржа:
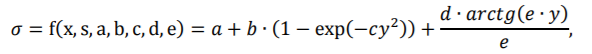
Обычно, модель подбирают в виде улыбки. Т.е. пересчитывают текущие бид-аски в стаканах (на всех страйках выбранной опционной серии) в IV и подбирают такие параметры модели, чтобы ее улыбка примерно лежала между бид-асками:
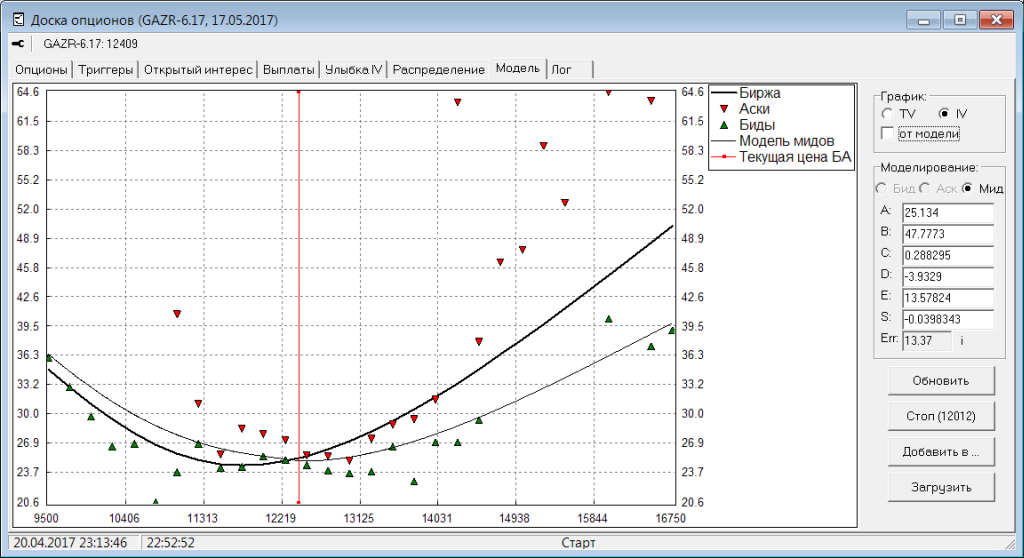
(жирная линия - улыбка подобранная биржей, тонкая линия - самостоятельный подбор)
При таком подборе есть проблема: нужно назначать разный вес ошибки подбора для центральных страйков и для страйков на краях улыбки. Поскольку на краях даже большая ошибка в IV на самом деле дает небольшую погрешность в пунктах. И наоборот: даже небольшая ошибка в IV на центральном страйке - выливается в большую погрешность в пунктах. Биржа учитывает это в своем алгоритме подбора улыбки, но иногда он дает сбой и биржа начинает выдавать улыбку хорошо подогнанную на краях, но плохо на центре.
Поэтому можно попробовать подгонять модель не по IV, а непосредственно по стоимости опционов в пунктах. Вот предыдущий график, выраженные не в IV, а во временной стоимости (из котировок опционов вычитаем внутреннюю стоимость опциона):

Этот график слегка напоминает график плотности распределения вероятностей и уже по нему можно догадаться про основной принцип: временная стоимость опциона на каком-либо страйке зависит от вероятности экспирироваться на этом уровне или дальше. Чем ближе страйк к текущей цене БА, тем больше стоимость опциона. И наоборот. А уже вероятность зависит и от времени до экспирации, и от текущей волатильности БА, и от ожиданий гэпов и т.д. Но первична тут именно вероятность. Далее мы попытаемся доказать, что торговля опционами в общем смысле - это торговля вероятностями, а не волатильностью, как это обычно считается.
Вернемся к приведенному выше графику. По нему видно - насколько важно подгонять модель на центральных страйках, а не на краях. Но на таком графике плохо видно - насколько хорошо вписалась модель между бид-асками. Гораздо удобнее взять модель за ноль (т.е. из всех цен вычитать справедливую цену, которую выдает модель). Получается такой график:

Здесь уже хорошо видно, насколько удачно вписалась модель в рынок, и на каких страйках потенциально можно покупать или продавать опционы (относительно модели). Также здесь видно, насколько наша модель отличается от подобранной биржей (черная жирная линия). Если бы модели совпадали, то черная линия была бы горизонтальной на нулевом уровне.
Итак, подобрав модель под текущие бид-аски на рынке, мы получаем свободу и можем по этой модели вычислять хоть цены опционов (на любых страйках, даже несуществующих на бирже), хоть улыбку IV, хоть распределение вероятностей где окажется цена БА на экспирацию:

Какие же возможности нам может дать использование распределения вероятностей? Во-первых, мы можем вычислить вероятности экспирации выше или ниже каких-то страйков по мнению рынка. И если мы с этим мнением не согласны - вступить в спор с рынком (открыв соответствующую позицию). Во-вторых, имея распределение вероятностей, мы можем по нему вычислить различные оценки для любой опционной позиции (вероятность безубытка, матожидание PnL, вероятность краха или посчитать VaR, и многое другое):

В третьих, оформив собственный прогноз в виде распределения вероятностей и учитывая текущие цены на рынке, мы можем подобрать оптимальную опционную позицию под наше вью и даже точно вычислить оптимальную долю счета (OptF), которую нам нужно использовать под открытие этой позы. Все это нам недоступно, если мы используем только улыбку волатильности (которая, как мы показали в прошлой статье, является просто набором поправочных коэффициентов).
Итак: использование распределения вероятностей дает нам больше возможностей и позволяет более осознано торговать опционами.
Ссылки по теме: