Оптимальная доля счета (OptF)
Итак, на последнем занятии мы выяснили, что есть возможность, посмотрев на котировки опционов на разных страйках увидеть не только и не столько подразумеваемую волатильность, а РАСПРЕДЕЛЕНИЕ вероятностей, которое рынок подразумевает в настоящий момент. Соответственно, мы вправе иметь собственное мнение по поводу того, с какой вероятностью рынок будет расти и до какого уровня или падать.
Имея свое распределение вероятности мы в состоянии оценить произвольную опционную позицию на нем и вычислить для этой позиции несколько интересных и полезных для процесса трейдинга параметров – вероятность безубытка, прибыль/убыток соотношение, вероятность катастрофических потерь, VaR и т.д. Что поможет нам искать наилучшую позицию для нашего прогноза.
Но тут есть одно "но". Когда мы собираемся открыть позицию, то важно не только определить состав позиции (лонг/шорт БА для линейной торговли, или какая-то сложная комбинация опционов при нелинейной), но и вычислить оптимальную долю счета, которую мы будем задействовать. Чтобы лучше понять насколько важна эта доля - рассмотрим игру, которую предложил Ральф Винс в своей книге «Математика управления капиталом». Ставим на кон какую-то долю от счета и с вероятностью 50% либо утраиваем поставленные деньги, либо их проигрываем. Матожидание у такой игры положительное (0.5*2 - 0.5*1=+0.5), и очевидно, что тут можно хорошо заработать. Но вот какую долю от имеющихся денег ставить каждый раз на кон? Если делать слишком маленькую ставку, то выигрыш будет, но небольшой, и пользы будет мало. Если увеличивать долю поставленных денег, то счет будет расти все быстрее. Но, с другой стороны, если поставить слишком большую долю, например, каждый раз ставить всю имеющуюся сумму, то с вероятностью 50% она будет потеряна. Т.е. игра для нас окажется совсем не полезной. В книге Ральфа Винса утверждается, что золотой серединой будет 1/4 от счета. Автор назвал эту долю оптимальное F (OptF).
Смоделируем эту игру в программке, которая эмулирует большое кол-во сделок для заданного F (используемая доля счета): 0.01, 0.02, ..., 0.99, 1.00. И для каждого такого F считает TWR (во сколько раз увеличился/уменьшился счет после всех сделок). Вот какой график получается:
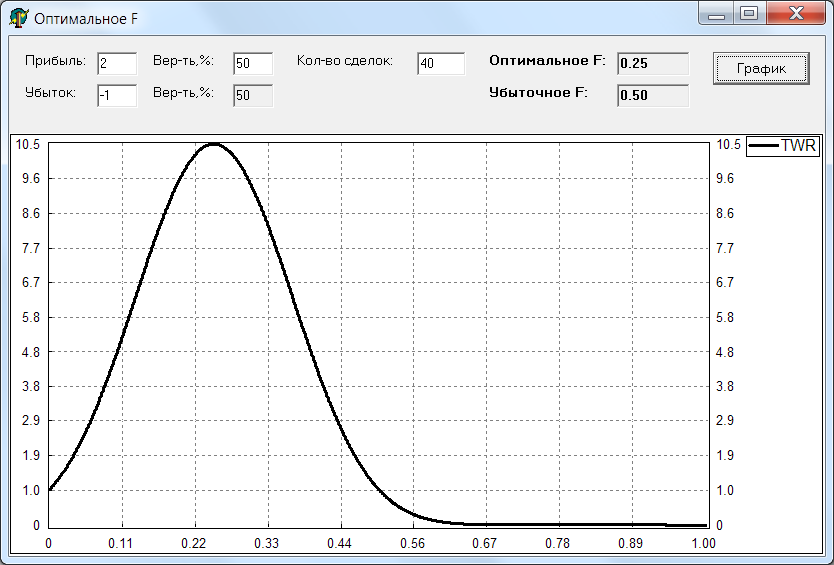
Видно, что максимум TWR достигается при F = 0.25 и равен 10.5 (весь счет увеличился в 10.5 раз за 40 сделок). Интересно, что при F > 0.5 счет начинает не расти, а убывать (TWR < 1). Значит, если ставить каждый раз на кон более половины счета, то при достаточном кол-ве сделок счет неизбежно будет слит. Хотя матожидание сделок - положительное. Вот такой парадокс.
Чтобы можно было вычислить оптимальное F не прибегая к моделированию сделок, используем функцию полезности. Она будет показывать для каждого прироста счета, насколько это приращение было полезно для нас. В качестве такой функции возьмем: U = Ln(1 + R), где U - полезность, R - доходность трейда. Вот график:
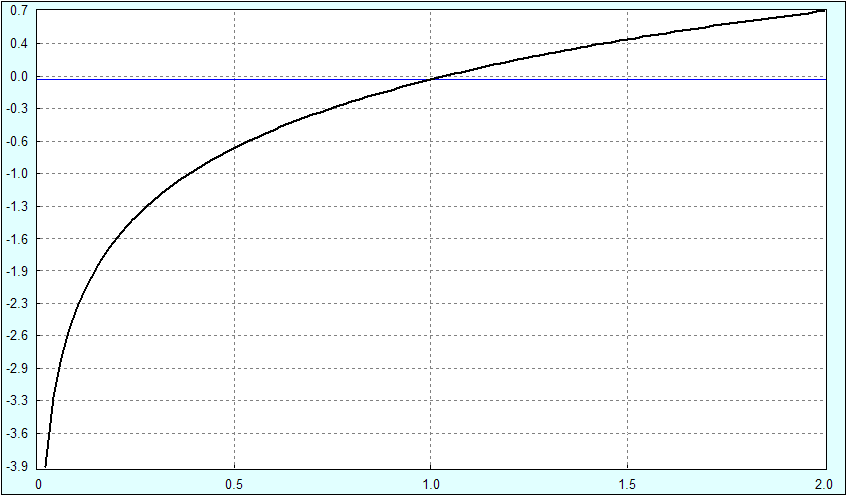
Когда доходность R = 0, то полезность U = 0. Если доходность положительная, то полезность начинает плавно расти. Если доходность отрицательная, то полезность с ускорением устремляется к минус бесконечности. Такая функция полезности соответствует резкому неприятию риска. Но у инвестора может быть и другое отношение к риску: умеренное или даже наоборот жажда риска. Для каждого подхода будет своя ф-ция. Подробнее о функциях полезности - см. Свойства функций полезности из книги Новый подход к управлению капиталом Ральфа Винcа.
Итак, имея функцию полезности, мы можем посчитать ее значения для каждого возможного исхода игры. А используя распределение вероятностей этих исходов, можем посчитать матожидание этой функции на заданном распределении, т.е. как бы среднюю полезность. И можем это сделать для каждого возможного значения F, от 0 до 1. Назовем новую функцию: МОП (МатОжиданиеПолезности). Вот какой у нее получается график для рассматриваемой игры (нормировка к масштабу графика TWR):

Видно, что максимум функции МОП совпадает с максимумом функции TWR. При F = 0 и 0.5 МОП равна нулю, т.е. при таких ставках мы не будем ни зарабатывать, ни терять деньги. При F > 0.5 матожидание полезности < 0, соответствует тому, что счет будет таять и при достаточном кол-ве сделок будет неизбежно слит.
Посмотрим, теперь что происходит, если матожидание торговли - нулевое или отрицательное. Вот график МОП (слева матожидание = 0, справа - отрицательное):
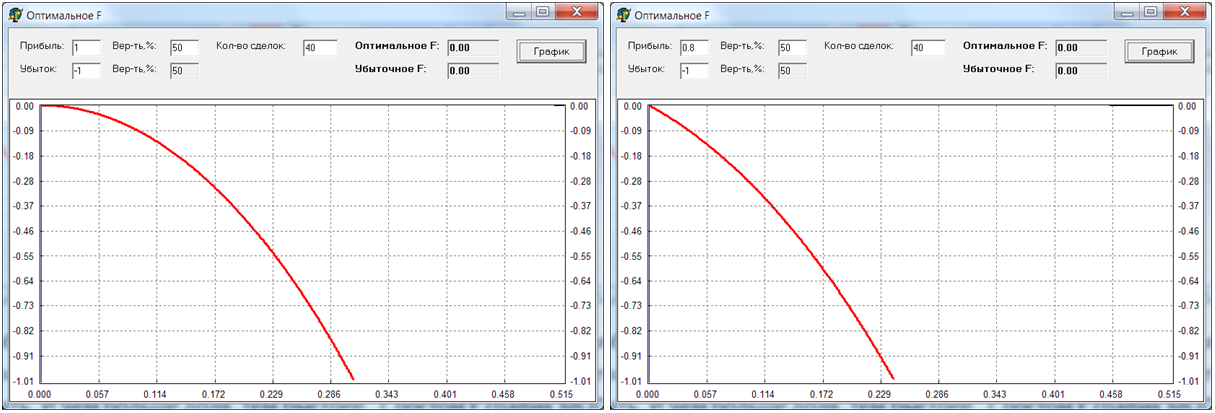
Видно, что в обоих случаях OptF = 0, т.е. математика советует вообще не открывать позицию. Если же открываться даже на небольшую долю, то счет будет неизбежно таять. Система с отрицательным матожиданием отличается только скоростью слива.
Эти графики показывают судьбу любого игрока, который совершает спорадические сделки без всякой системы (под влиянием интуиции, советов различных аналитиков, и т.д.). Если составить распределение результатов его сделок (какие-то будут в плюс, какие-то в минус), то скорее всего получится распределение с нулевым матожиданием. Вспомнив про накладные расходы (комиссии, спред, и т.д.), получим систему с отрицательным матожиданием. Если такой трейдер достаточно осторожен и открывается только на небольшую долю счета, то слив будет медленным и постепенным. Если он бесшабашен и открывается "на всю котлету", то его МОП будет стремится к минус бесконечности. Т.е. буквально несколько сделок и счету - конец.
Здесь можно вспомнить еще такую идею: заключить союз с неудачливым трейдером, постоянно торгующим в убыток, и совершать противоположные ему сделки. Казалось бы, результат такой торговли должен быть положительным. Но - нет, тут нет грааля. Если такой трейдер торгует с нулевым матожиданием (до вычета накладных расходов), то и противоположная торговля тоже будет с нулевым МО. А с учетом комиссий - опять получится система с отрицательным матожиданием. И судьба такой торговли наоборот - такая же. Как на графике выше.
Существуют ли в принципе системы с положительным матожиданием? Очевидно, что в HFT такие системы есть. Но там большая конкуренция, дорогая инфраструктура, погоня за микросекундами, продвинутые математики и т.д. Можно ли найти положительное МО в обычной торговле, без HFT? На этот счет есть разные мнения. Те, кто верит, что рынок всегда эффективен, утверждают что таких систем нет. Другие утверждают, что человек несовершенен (страх, жадность, и т.д.) и в некоторые моменты толпа на рынке бывает неправа и возникают неэффективности. Оставим пока этот вопрос открытым и вернемся к нему позже.
Пока же вернемся к опционам и рассмотрим вопрос с OptF уже в применении к опционной торговле. Применяя ту же технику, вычисляем МОП на распределении вероятностей и находим оптимальное F. Максимальное МОП, соответствующее этому F, примем за общую оценку позиции. Чем больше матожидание полезности у комбинации, тем лучше (полезнее) для нас эта комбинация.
Рассмотрим пример. Допустим, мы больше чем рынок верим в рост и добавляем к рыночному распределению вероятностей более толстый хвост справа (делаем смесь рыночного распределения и нормального, у которого матожидание в сторону роста). Посмотрим - какие получились оценки для некоторого списка стандартных комбинаций:
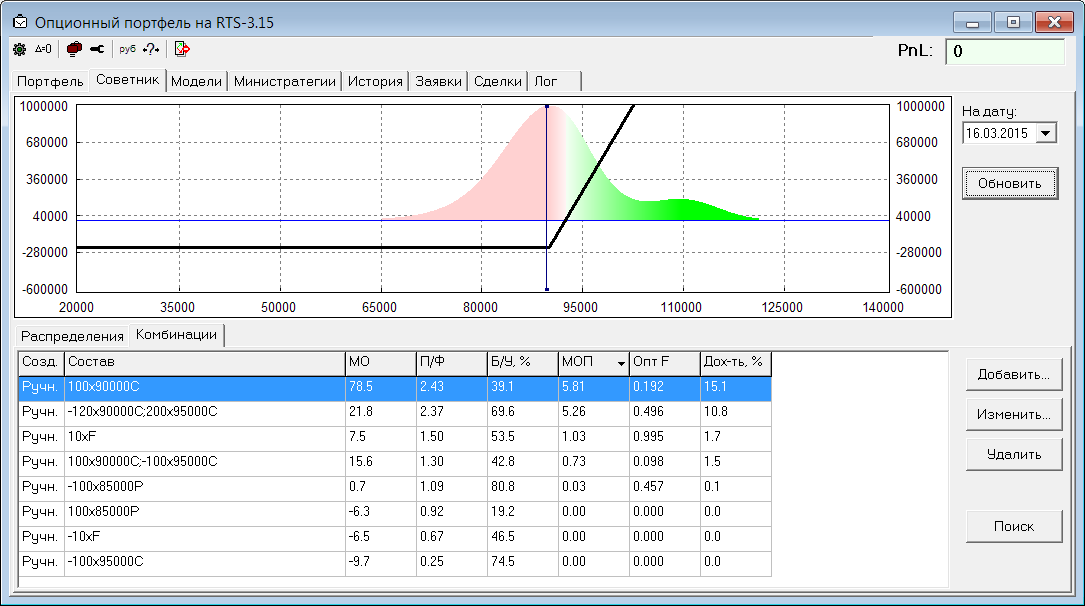
Из рассмотренных комбинаций самый большой МОП у купленного колл. Чуть похуже - у пропорционального обратного колл-спреда. Покупка просто голого фьюча - сильно отстает от первых двух позиций. Продажа пута, хоть и показывает положительное МО, но оценка МОП у него почти 0. Это из-за того, что функция полезности начинает стремится к минус бесконечности в левом хвосте. И хотя вероятность выйти в безубыток у этой позиции самая большая (80%), матожидание полезности говорит нам, что это самая слабенькая позиция (для нашего прогноза на рост). Три последних комбинации (покупка пута, продажа фьюча, продажа колла), как и должно быть, показывают отрицательное МО на нашем распределении, МОП у всех равен 0, OptF = 0, и естественно открывать эти позиции не нужно (если мы прогнозируем рост).
Вернемся к лучшей (среди рассмотренных) позиции: покупка колла. Вероятность безубытка тут небольшая, всего 40%. Но матожидание прибыли большое. У этой позиции OptF=0.192. Т.е. если такой колл стоит 100, а у нас на счету 1000, то самым оптимальным будет купить 2 колла. Если же не послушаться математики и купить, например, 9 контрактов (F = 0.9), то ожидаемая доходность, конечно, вырастет (с 15% до 70%), но теперь мы можем потерять 90% от счета (с вероятностью почти 60%). О чем нам и говорит новая оценка МОП этой позиции, которая стала хуже всех остальных:
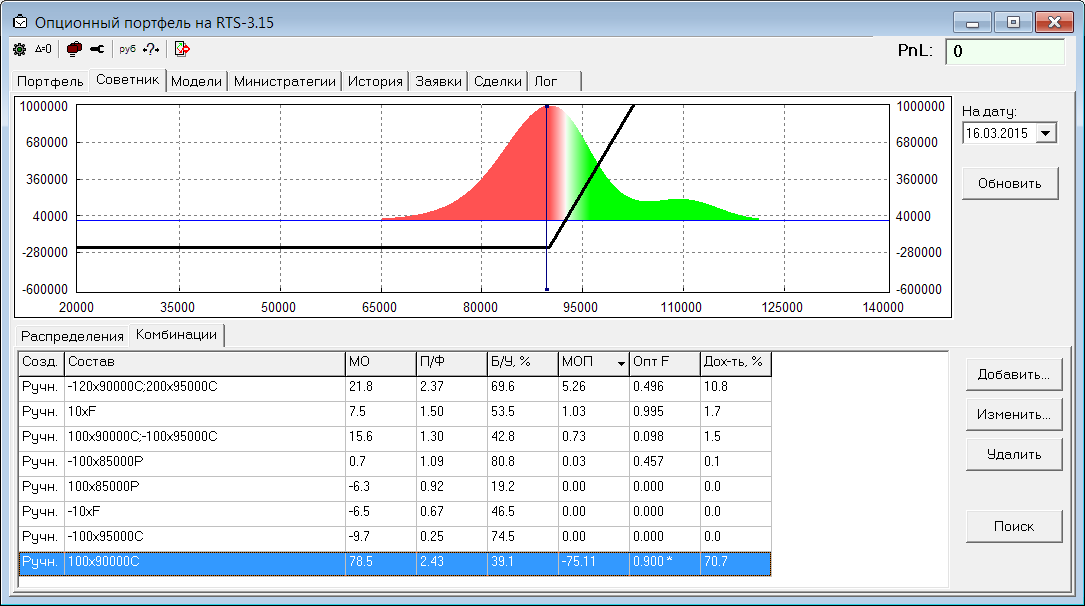
Это доказывает, что даже потенциально самую лучшую комбинацию можно превратить в очень плохую (не полезную) для счета позицию, если открыть ее слишком большим объемом.
Подведем итоги:
- Нужно искать системы с положительным матожиданием.
- Найдя систему с положительным матожиданием, нужно вычислять OptF и стараться не превышать эту долю.
- Торговать систему с нулевым матожиданием (и тем более с отрицательным) - нельзя.
- Если у нас есть распределение вероятностей (в которое верим), и есть функция полезности (которая отражает наши предпочтения к риску), то для любой опционной позиции можно точно вычислить ее оптимальный объем.