Улыбка волатильности
Итак, мы начинаем торговать опционами. Мы видим в стакане котировки на каждом страйке – заявки на покупку и заявки на продажу. Справедливы ли цены, указанные в заявках? Как самому составить представление о справедливой цене на опцион?
Аксиома биржевой торговли гласит, что биржевой аукцион максимально близко определяет то, что цена на торгуемый товар, сложившаяся в настоящий момент, справедлива! И, что тоже совершенно очевидно, в следующий момент времени на тот же товар обязана сложиться новая, но справедливая цена. Эта цена зависит от многих факторов и ее значение в пунктах может меняться быстро и очень значительно. Поэтому обычно вместо самой цены используют другую величину: IV. Которую называют подразумеваемой волатильностью опциона (implied volatility). Ее значение вычисляют используя формулу Блэка-Шоулза, в которую подставляют несколько параметров (текущую цену БА, стоимость опциона в пунктах, его страйк, время до экспирации, Колл или Пут; еще в формуле присутствует безрисковая ставка, но на наших маржируемых опционах ее считают нулевой). IV опциона меняется уже гораздо меньше, чем цена в пунктах и это достаточно удобно. Можно выставить в программе заявку: купить или продать опцион по такой-то IV и уйти от терминала. Программа будет сама пересчитывать цену заявки в пунктах и переставлять ее в зависимости от текущей цены БА и времени до экспирации.
Если пересчитать рыночные цены опционов на каждом имеющемся страйке в IV и отобразить эти значения графически - получится так называемая улыбка IV:
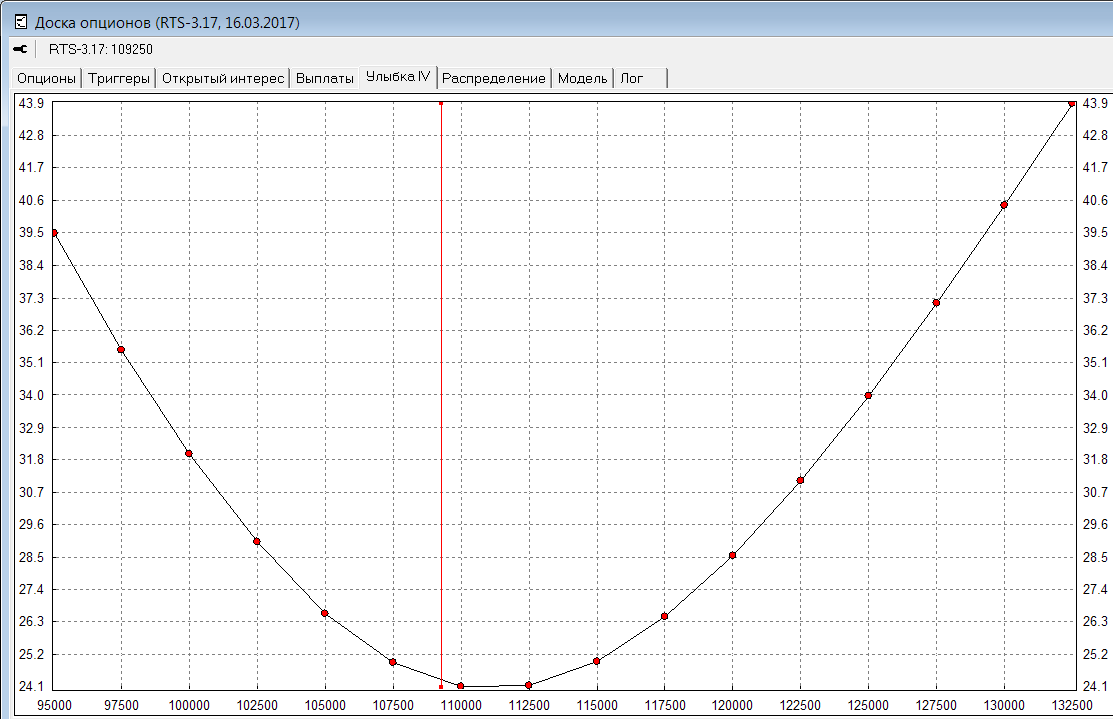
Откуда это явление? Можно ли, торгуя опционом, подразумевать для себя разную волатильность на разных страйках? Конечно нет. Улыбка IV получается при использовании формулы Блека-Шоулза, а ключевое предположение модели Б-Ш: поведение цены подчиняется модели геометрического броуновского движения. Т.е. приращения логарифмов цены должны быть распределены нормально. Но это предположение совершенно точно не выполняется на реальном рынке. Вот, к примеру, распределение приращений для фьючерса на индекс RTS (для сравнения добавлено нормальное распределение с такой же дисперсией):
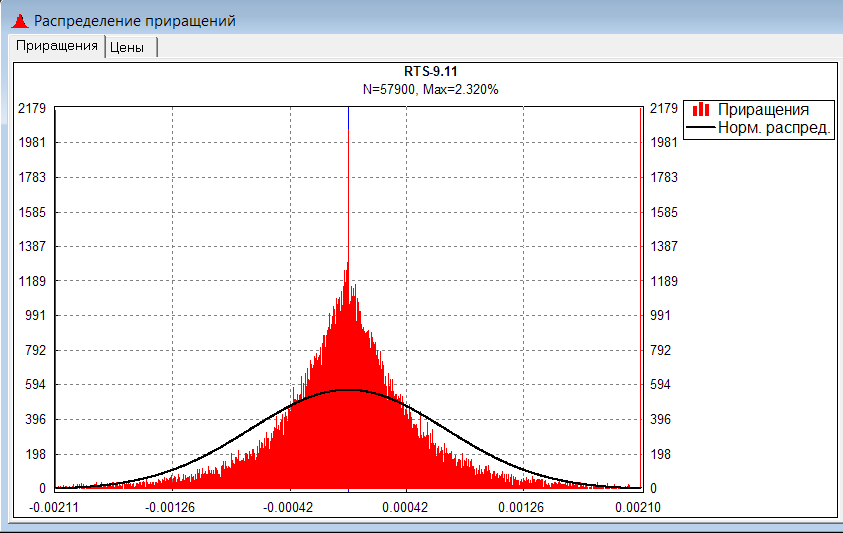
Видно, что реальное распределение значительно отличается от нормального. Во-первых, частота маленьких приращений (боковик) гораздо выше, чем предполагается нормальным распределением. Во-вторых, сильные движения (гэпы) и по размеру и по частоте тоже совсем не вписываются в нормальное распределение.
Соответственно, не будет выполняться и предположение о распределении вероятностей, где окажется цена БА на экспирацию. В теории БШ предполагается, что оно будет логнормальным. И хотя, если мы возьмем только какой-то один страйк, то мы можем подобрать такое логнормальное распределение, которое будет соответствовать текущей рыночной цене. Вот пример для страйка 120000:
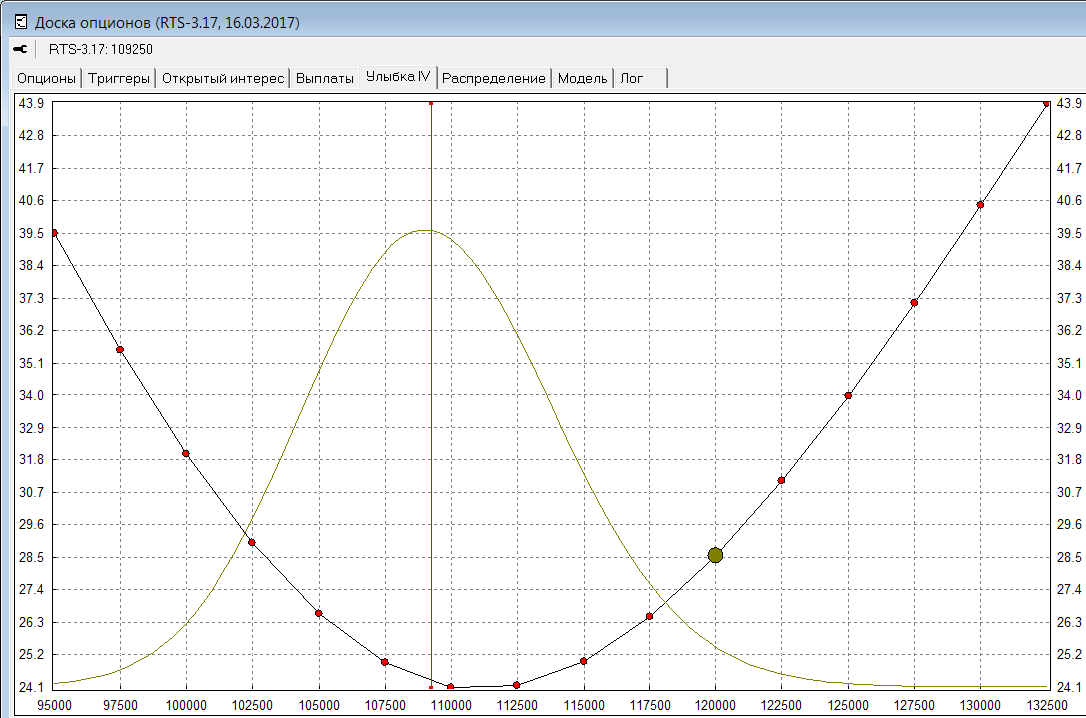
Но если мы возьмем другой страйк, то нам потребуется уже другое распределение, чтобы посчитанная по нему справедливая цена соответствовала текущему рынку. И так для каждого страйка. Вот графики логнормальных распределений для 4х страйков:
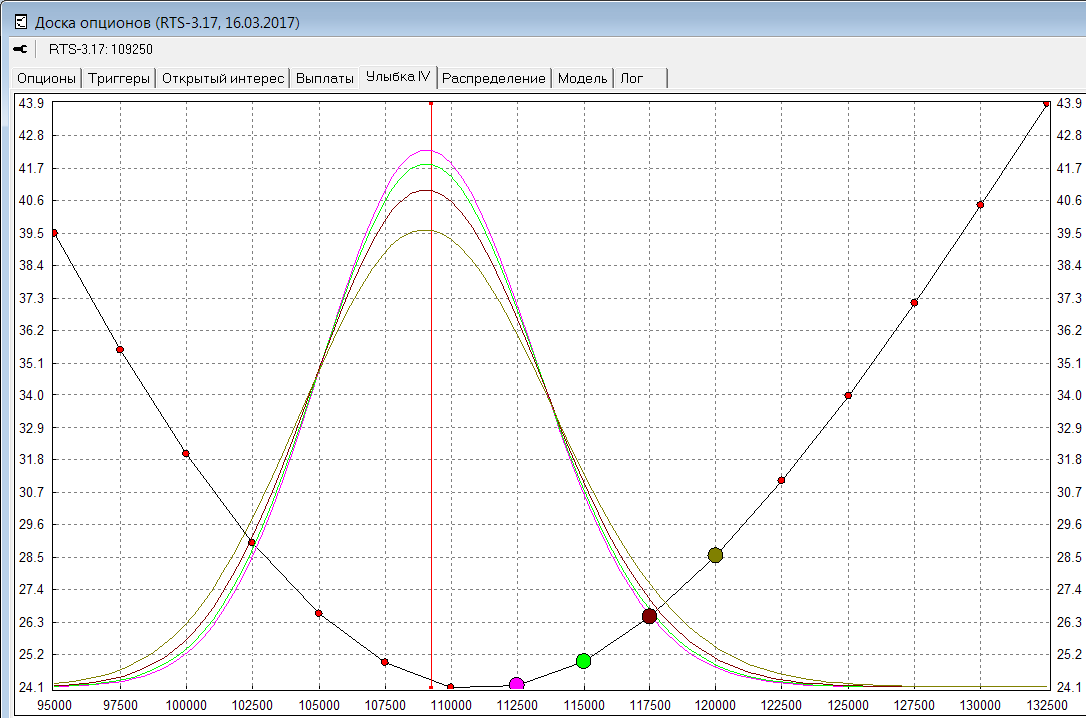
Видно, что на каждом страйке нам приходилось брать распределение с другой дисперсией (чем больше IV, тем больше дисперсия). Получается множество распределений вероятностей, прогнозирующих одну цену (где будет БА на экспирацию). Хотя, если мы останавливаемся на каком-то одном случайном процессе, то оно дает только одно распределение. И оно не должно зависеть от того, на каком страйке мы хотим посчитать справедливую цену. Существует возможность для текущих рыночных цен опционов (на всех страйках какой-то одной выбранной серии) подобрать одно такое распределение (назовем его рыночным и обозначим Q), подсчет справедливой стоимости по которому для любого страйка будет соответствовать рыночной цене. Подробнее о том как подбирать такое распределение и какое преимущество оно может дать - поговорим на следующих уроках. Пока же посмотрим его график (функция плотности рыночного распределения - черная жирная линия):
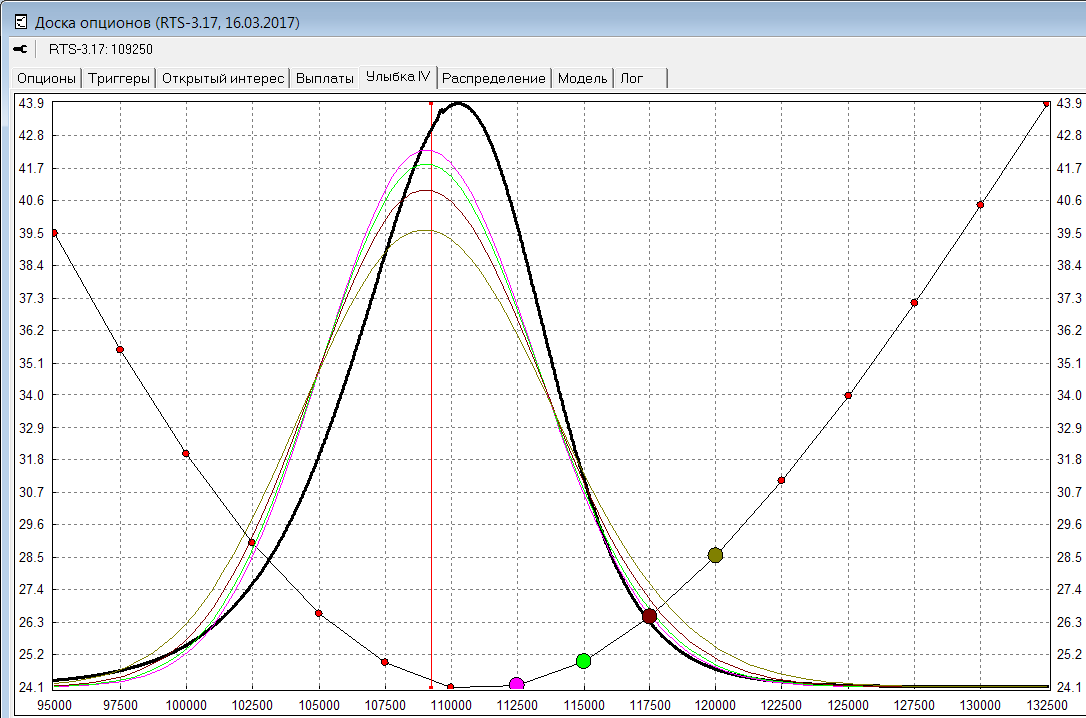
Видно, что все логнормальные распределения, предполагаемые моделью Б-Ш, отличаются от рыночного.
Подведем итог: улыбка волатильности является ничем иным, как просто набором поправочных коэффициентов, чтобы преобразовывать теоретические логнормальные распределения в реальное рыночное. Т.е. улыбка - это не объект физической природы, а в каком-то роде "костыль", с помощью которого неправильная модель Б-Ш подгоняется по рынок. В следующих уроках мы покажем, что лучше работать не с улыбкой, а напрямую с реальным рыночным распределением.