Оценка опционных позиций – что такое хорошо и что такое плохо?
Итак, у нас есть распределение вероятностей по мнению рынка и у нас есть распределение вероятностей, которое по нашему мнению точнее прогнозирует цену БА на экспирацию. Как воспользоваться этими знаниями? Как найти опционную позицию, наилучшим образом соответствующую нашему прогнозу, текущим ценам на рынке и нашему отношению к риску?
Так вот, ответ на вопрос, «что лучше?» – субъективен. Допустим, мы даем больше вероятности на рост, чем подразумевает сейчас рынок. Как минимум, два варианта сразу приходят на ум. Можно продать PUT, а можно купить CALL. Мы пытаемся вычислить, где доход побольше, но одновременно боимся – если наш прогноз не оправдается, будут ли убытки. Что для нас важнее – доход любой ценой или чуть заработать, лишь бы не потерять?
На самом деле, параметров, характеризующих опционную позицию с точки зрения потребительских свойств, ещё больше. Вот самые интересные:
- Вероятность безубытка.
- Математическое ожидание прибыли и убытка (PnL).
- Сумма под риском (VaR).
- Вероятность катастрофических потерь.
Итак, если мы попытаемся оптимизировать опционную позицию по всем четырем параметрам, пытаясь максимизировать параметры 1 и 2 и минимизировать параметры 3 и 4, мы получим некое четырехмерное пространство решений, в котором нам, как трейдерам, будет трудно сориентироваться. Вспомним совет Кирилла Ильинского из лекции про финансовые модели: "Ответ должен быть всегда одно число". Попытаемся сделать это и привлечем на помощь теорию полезности. Мы заведем функцию полезности, которая будет по-разному оценивать наши возможные убытки и прибыли. Обычно, в качестве функции полезности советуют использовать натуральный логарифм: U = Ln(1 + R), где U - полезность, R - доходность трейда. Большинство людей психологически не приемлют убыток, гораздо сильнее переживают его эмоционально, нежели испытывают удовольствие от роста дохода. Вот график такой функции:
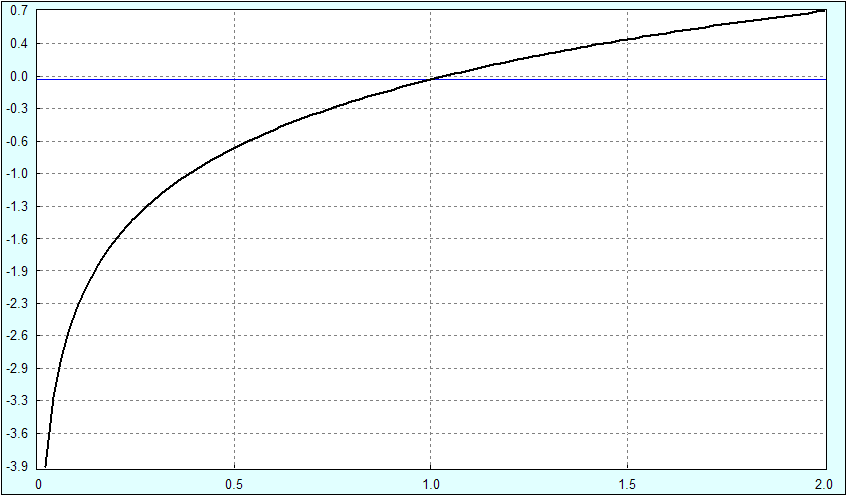
Когда доходность R = 0, то полезность U = 0. Если доходность положительная, то полезность начинает плавно расти. Если доходность отрицательная, то полезность с ускорением устремляется к минус бесконечности. Такая функция полезности соответствует резкому неприятию риска. Но, кстати, у инвестора может быть и другое отношение к риску: умеренное или даже наоборот жажда риска. Для каждого подхода будет своя функция. Подробнее о функциях полезности - см. Свойства функций полезности из книги Новый подход к управлению капиталом Ральфа Винcа.
Теперь, имея функцию полезности, мы можем просто проинтегрировать ее значения для заданной опционной позиции на заданном распределении вероятностей (посчитать матожидание полезности) и получить одно число. Т.е. мы получили способ, с помощью которого можно оценить любую опционную позицию. И теперь можем для каждой позиции получать одно число, которое будет ее полностью оценивать. Чем выше оценка - тем лучше позиция. Все что для этого требуется - оформить свой прогноз в виде распределения вероятностей и задать функцию полезности, соответствующую нашему отношению к риску. И мы получаем строгий математический инструмент, позволяющий сравнить между собой произвольные опционные позиции и выявить - какая лучше.
Ссылки по теме: