Распределение вероятностей и матожидание

Предположим, цена движется в канале и достигла линии поддержки. Опыт торговли подсказывает нам, что вероятность «отскока» 60%, а вероятность пробоя линии поддержки вниз, до следующего уровня – 40%. Достаточно ли этого знания для принятия эффективных торговых решений? Безусловно нет. Давайте рассмотрим два упрощенных примера:

1. 60% вырастет на 100 пунктов, 40% упадет на 100 пунктов.
2. 60% вырастет на 100 пунктов, 40% упадет на 200 пунктов.

Т.е. в первом случае отскок от линии поддержки и пробой будут равны. А во втором - пробой в два раза больше отскока.

Если мы будем руководствоваться только знанием о вероятности, то наше решение будет - в обоих случаях открывать лонг позицию. Но если посчитать математическое ожидание:

1. (0.6*100 - 0.4*100)/2 = +10п
2. (0.6*100 - 0.4*200)/2 = -10п

Получается, если мы хотим только один раз совершить сделку (и больше потом никогда не торговать по этой системе), то нам нужно смотреть на вероятность. И когда система подаст такой сигнал - покупать, на следующем приращении закрыть позицию, и больше по этой системе не торговать. С вероятностью 60% мы будем в плюсе. Если же мы собираемся регулярно торговать по нашей системе, то нам становится важна не вероятность, а матожидание результата. Важен будет не отдельный трейд (открытие позиции и потом закрытие), а что будет в среднем. И тогда в первом примере нам нужно покупать, а во втором - продавать. Вот как выглядят распределения вероятностей в этих двух примерах:

60% +100п, 40% -100п	60% +100п, 40% -200п
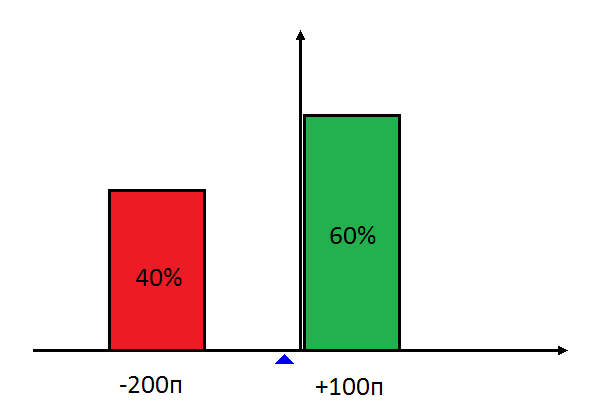Матожидание +10п -> нужно покупать	Матожидание -10п -> нужно продавать

Обратите внимание на маленький синий треугольник под каждым распределением. Он указывает - где находится матожидание распределения. Если мы возьмем, например, красный столбик и не меняя его вероятность (40%) будем просто двигать его влево или вправо (менять распределение этой вероятности), то матожидание распределения (точка равновесия) будет меняться.

Здесь сделаем небольшое отступление и покажем где визуально находится матожидание распределения, а заодно и его мода и медиана. У симметричного распределения матожидание находится прямо под пиком (модой). У несимметричного получается так:

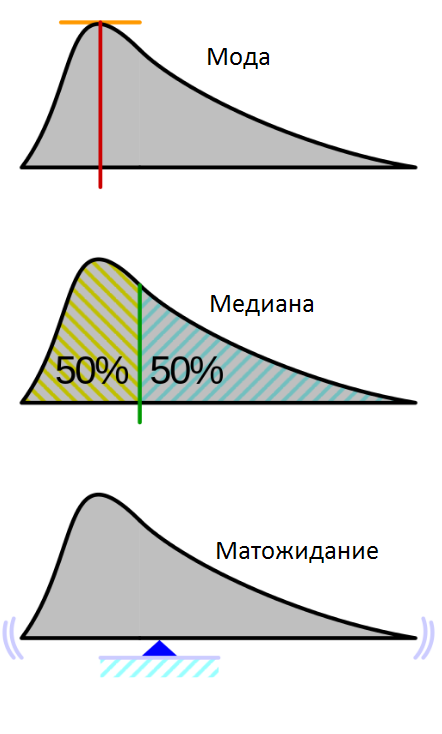
Т.е. если бы мы вырезали из фанеры распределение, то матожидание будет в точке, где вырезанная фигура будет уравновешена.

Итак, в случае регулярной торговли, одной только вероятности о дальнейшем движении цены - мало. Нужно знать - как эта вероятность распределяется. И разные распределения могут рекомендовать диаметрально противоположные позиции. Кроме того, разные распределения будут советовать и разную долю счета, которую будет рекомендовано использовать для открытия позиции. Это не менее важный момент, чем состав позиции. Например, у нас есть система с положительным матожиданием. На каждые поставленные 1000р она обещает в среднем +10р, вероятность прибыльного трейда 60%, убыточного 40%. Наш счет 1 000 000р. Если мы открываемся на 1000р, то в среднем на каждый трейд будем получать 10р. Если на 10 000р - получим 100р. На 100 000р - ожидаем 1000р. Казалось бы, чем больше мы поставим - тем лучше. Система то с положительным матожиданием. Однако, если мы поставим все имеющиеся деньги, то с вероятностью 40% можем их целиком потерять. Т.е. мы можем повышать ставку, но только до какого-то предела. Называется этот предел - оптимальная доля счета, OptF. И его легко посчитать по распределению вероятностей. Подробнее об этом расcкажем на отдельном уроке. Пока же продемонстрируем только график, который иллюстрирует вопрос с OptF:

На оси Х тут - используемая доля счета: от нуля (ничего не используем), до 1 (используем все деньги на счете целиком). Функция TWR - показывает во сколько раз изменится кол-во денег счету в зависимости от используемой доли счета. Видно, что на промежутке [0, 0.2] чем больше доля счета, тем больше растет счет. Но после 0.2 рост счета прекращается и на уровне 0.4 счет начинает таять (TWR < 1). Т.е. для данной системы OptF=0.2, и мы должны открываться не больше чем на 1/5 от счета.

Из приведенных примеров видно - как важно распределение даже для линейной торговли БА, разные распределения диктуют разные позы: лонг в первом случае, и шорт во втором. И что не менее важно - позволяет вычислить OptF. Тем более распределение вероятностей оказывается важным для нелинейной торговли - опционами.